Question

Consider the water balance for a 12 km2 watershed that has the following known inputs

and outputs: annual precipitation 650 mm, annual evapotranspiration 230 mm, and the
average annual discharge for the stream draining the watershed is 0.15 m3
/s.
a. Calculate the net change in the volume of storage (i.e. the water balance), and
express your answer in mm of depth. Clearly explain any assumptions you have to
make. (5 marks)
b. Discuss if you think that renewable water resources in this watershed may be at
risk in the face of climate warming. (2 marks)

Answer 1

a) The net change in the volume of storage is 5.039 million cubic meters.

b) Climate warming may lead to an increase in evapotranspiration rates and a decrease in precipitation rates, reducing net change in the volume of storage and putting that renewable water resources at risk.

Step-by-step explanation:

a) The net change in the volume of storage (
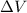`\Delta V`), measured in cubic meters, is the sum of inputs and outputs in the watershed, represented by the following expression:

`\Delta V = V_(p) -V_(e)-V_(d)` (1)

Where:

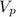`V_(p)` - Added volume due to precipitation, measured in cubic meters.

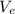`V_(e)` - Subtracted volume due to evapotranspiration, measured in cubic meters.

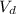`V_(d)` - Subtracted volume due to discharge, measured in cubic meters.

Let suppose that level changes are so small in comparison with the depth of the watershed, then we expand the equation below:

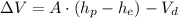`\Delta V = A\cdot (h_(p)-h_(e))-V_(d)` (1b)

Where:

`A` - Watershed area, measured in square meters.

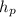`h_(p)` - Precipitation, measured in meters.

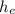`h_(e)` - Evapotranspiration, measured in meters.

If we know that
`A = 12* 10^(6)\,m^(2)`,
`h_(p) = 0.65\,m`,
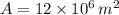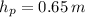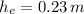`h_(e) = 0.23\,m` and
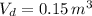`V_(d) = 0.15\,m^(3)`, then the net change in the volume of the storage is:

`\Delta V = (12* 10^(6)\,m^(2))\cdot (0.65\,m-0.23\,m)-0.15\,m^(3)`

`\Delta V = 5.039* 10^(6)\,m^(3)`

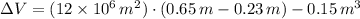
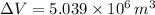
The net change in the volume of storage is 5.039 million cubic meters.

b) Climate warming may lead to an increase in evapotranspiration rates and a decrease in precipitation rates, reducing net change in the volume of storage and putting that renewable water resources at risk.