Question

Rectangle A, B, C, D is graphed in the coordinate plane. The following are the vertices of the rectangle: A(-6, -4),  B(-4,-4), C(-4, -2), and D(-6, -2). What is the perimeter of rectangle A, B, C, D?

​

Answer 1

The perimeter of polygon with the given coordinates is 8 units

How to find the perimeter

The perimeter is solved by finding the length of each of the sides of the polygon, and adding them together.

Plotting the points showed that the polygon is a special type of rectangle known as square.

All the sides are equal and of length 2 units. (image is attached)

perimeter of the rectangle

= 2 + 2 + 2 + 2

= 8 units

Answer 2

Perimeter of rectangle ABCD = 9.64 units

Explanation:

The formula used to calculate perimeter of rectangle is:

`Perimeter\: of\: rectangle=2(Length+ Width)`

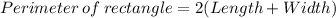
We know that rectangle has opposite sides same i.e Length (AB and CD) are same and Width( AD and BD) are same

We need to find Length and Width to find the perimeter

So, if we find Length AB and Width AC we can find perimeter

Finding Length AB

The length AB can be found using distance formula:
`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

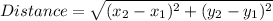
We have A =(-6,-4) and B(-4,-4)

So, x_1=-6, y_1=-4, x_2=-4, y_2=-4

Putting values in formula and finding length

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)\\Distance=√((-4-(-6))^2+(-4-(-4))^2)\\Distance=√((-4+6)^2+(-4+4)^2)\\Distance=√((2)^2+(0)^2)\\Distance=√(4+0)\\Distance = 2`

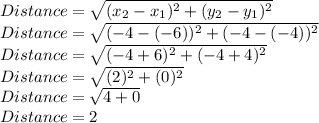
So, Length AB = 2

Now, Finding Width AC

The length AB can be found using distance formula:
`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

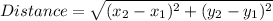
We have A =(-6,-4) and C(-4,-2)

So, x_1=-6, y_1=-4, x_2=-4, y_2=-2

Putting values in formula and finding length

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)\\Distance=√((-6-(-4))^2+(-4-(-2))^2)\\Distance=√((-6+4)^2+(-4+2)^2)\\Distance=√((-2)^2+(-2)^2)\\Distance=√(4+4)\\Distance = √(8)\\Distance=2.82`

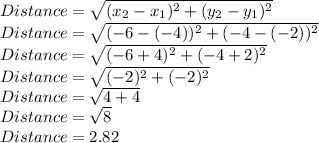
So, Width AD = 2.82

Now, We have Length = 2 and Width = 2.82

Finding perimeter of rectangle

`Perimeter\: of\: rectangle=2(Length+ Width)\\Perimeter\: of\: rectangle=2(2+ 2.82)\\Perimeter\: of\: rectangle=2(4.82)\\Perimeter\: of\: rectangle=9.64`

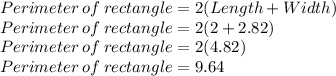
So, Perimeter of rectangle ABCD = 9.64 units