Question

A geometric series with 5 terms that begins with 8 and has a common ratio of 1/3.

The geometric series is...

The sum of the geometric series is...

Answer 1

The geometric series is
`8,(8)/(3) ,(8)/(9),(8)/(27),(8)/(81)`

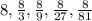
The sum of the geometric series is 12.06

Explanation:

First term of geometric series = 8

Common Ratio = 1/3

The formula used to find next term is:
`a_n=a_1r^(n-1)`

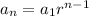
Our series has five terms, so we need to find 2nd, 3rd, 4th and 5th term

2nd term is:

`a_n=a_1r^(n-1)\\a_2=8((1)/(3))^(2-1)\\a_2=8((1)/(3))^(1)\\a_2=(8)/(3)`

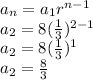
3rd term is:

`a_n=a_1r^(n-1)\\a_3=8((1)/(3))^(3-1)\\a_3=8((1)/(3))^(2)\\a_3=(8)/(9)`

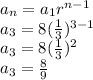
4th term is:

`a_n=a_1r^(n-1)\\a_4=8((1)/(3))^(4-1)\\a_4=8((1)/(3))^(3)\\a_4=(8)/(27)`

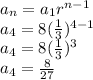
5th term is:

`a_n=a_1r^(n-1)\\a_5=8((1)/(3))^(5-1)\\a_5=8((1)/(3))^(4)\\a_2=(8)/(81)`

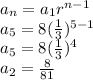
So, The geometric series is
`8,(8)/(3) ,(8)/(9),(8)/(27),(8)/(81)`

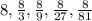
Now, Finding the sum of geometric series

The formula used is:
`S_n=(1-r^n)/(1-r)`

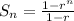
We have n =5, r=1/3

`S_n=(a(1-r^n))/(1-r)\\S_5=(8(1-(1)/(3)^5))/(1-(1)/(3) )\\S_5=(8(1-(1)/(243)))/(1-(1)/(3) )\\S_5=(8((243-1)/(243)))/((3-1)/(3) )\\S_5=(8((242)/(243)))/((2)/(3) )\\S_5=(8(0.995))/(0.66)\\S_5=12.06`

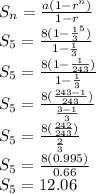
So, The sum of the geometric series is 12.06