Answer:
The geometric series is
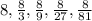
The sum of the geometric series is 12.06
Explanation:
First term of geometric series = 8
Common Ratio = 1/3
The formula used to find next term is:
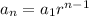
Our series has five terms, so we need to find 2nd, 3rd, 4th and 5th term
2nd term is:
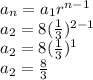
3rd term is:
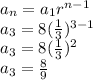
4th term is:
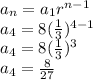
5th term is:
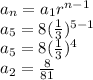
So, The geometric series is
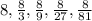
Now, Finding the sum of geometric series
The formula used is:
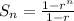
We have n =5, r=1/3
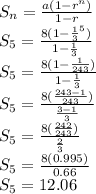
So, The sum of the geometric series is 12.06