Question

what are the explicit equation and domain for a geometric sequence with a first term of 5 and a second term of -10

Answer 1

`a_1=5;\ a_2=-10;\ r=a_2:a_2\to r=-10:5=-2\\\\a_n=a_1r^(n-1)\\\\\boxed{a_n=5\cdot(-2)^(n-1)}`

Answer 2

• The explicit equation is given by:

`a_n=5(-2)^(n-1)`

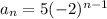
• The domain of the geometric sequence is: All the natural numbers (i.e. n≥1)

Explanation:

Explicit formula--

The explicit formula is a formula which is used to represent the nth term of a sequence in terms of the variable n.

It is given that:

The first term of the sequence is 5 and the second term is -10.

This means that if a denotes the first term and r denotes the common ratio.

The geometric sequence is given by: a,ar,ar²,ar³,....

i.e. the nth term of the sequence is given by:

`a_n=ar^(n-1)`

Then we have:

`a=5`

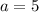
and

`ar=-10\\\\i.e.\\\\5* r=-10\\\\i.e.\\\\r=(-10)/(5)\\\\i.e.\\\\r=-2`

Hence, the nth term of the sequence is given by:

`a_n=5(-2)^(n-1)`

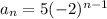
We know that the domain of a geometric sequence is the set of all the natural numbers.

( since the term a_n is defined for all the natural numbers ).