Question

What are the exact solutions of x2 - 3x - 1 = 0?

Answer 1

`x^2-3x-1=0\\a=1;\ b=-3;\ c=-1\\\\\Delta=b^2-4ac\\\Delta=(-3)^2-4\cdot1\cdot(-1)=9+4=13 \ \textgreater \ 0\\\\x_1=(-b-\sqrt\Delta)/(2a)\ and\ x_2=(-b+\sqrt\Delta)/(2a)\\\\\sqrt\Delta=√(13)\\\\x_1=(-(-3)-√(13))/(2\cdot1)=(3-√(13))/(2)\\\\x_2=(-(-3)+√(13))/(2\cdot1)=(3+√(13))/(2)`

Answer 2

`x_(1)=(-3+√(13) )/(2)\\`

`x_(2)=(-3-√(13) )/(2)\\`

Explanation:

the equation is:
`x^2-3x-1=0`

you have a quadratic equation of the form:

`ax^2+bx+c=0`

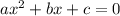
where
`a=1,b=-3,c=-1`

this can be solved using the general formula:

`x=(-b+-√(b^2-4ac) )/(2a)`

substituting all the known values:

`x=(-(-3)+-√((-3)^2-4(1)(-1)) )/(2(1)) \\x=(-3+-√(9+4) )/(2)\\ x=(-3+-√(13) )/(2)\\`

one value for x will be found using the plus sign before the square root:

`x_(1)=(-3+√(13) )/(2)\\`

and the other will be found using the negative sign before the square root:

`x_(2)=(-3-√(13) )/(2)\\`