Explanation
To find the domain from the graph, you have to focus only x-axis because domain is the set of x-value.
From the graph, we can see that domain starts at x = 0 and keeps going and going positive infinitely. That means the domain must be greater or equal to 0.
Here is an easier way to understand
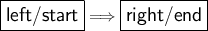

And if we combine both, we get

But we don't usually write positive infinity, therefore we convert to

Answer
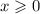
If you have any questions related to this answer, feel free to ask in comment.