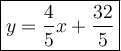Step-by-step explanation
- Find the slope by using rise over run with two given coordinate points.
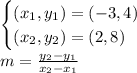
- Substitute the coordinate values in.
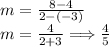
We have got the value of slope. Substitute in the slope-intercept form.
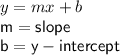
Substitute and Rewrite the equation.
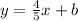
- Find the y-intercept or the value of b by substituting any given coordinate points.
I will substitute (2,8) in.
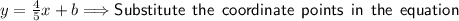
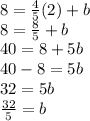
Rewrite the equation by substituting the value of b.
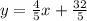
Answer