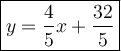Question

What is the equation of a line that passes theough the points (-3,4) and (2,8)?​

Answer 1

Step-by-step explanation

• Find the slope by using rise over run with two given coordinate points.

`\begin{cases} (x_1,y_1)=(-3,4) \\ (x_2,y_2)=(2,8) \end{cases} \\ m = (y_2 - y_1)/(x_2 - x_1)`

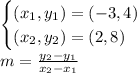
• Substitute the coordinate values in.

`m = (8 - 4)/(2 - ( - 3)) \\ m = (4)/(2 + 3) \Longrightarrow (4)/(5)`

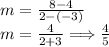
We have got the value of slope. Substitute in the slope-intercept form.

• Slope-Intercept

`y = mx + b \\ \sf{m = slope}\\ \sf{b = y - intercept}`

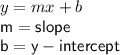
Substitute and Rewrite the equation.

`y = (4)/(5) x + b`

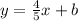
• Find the y-intercept or the value of b by substituting any given coordinate points.

I will substitute (2,8) in.

`y = (4)/(5) x + b \Longrightarrow \sf \small{Substitute \: \: the \: \: coordinate \: \: points \: \: in \: \: the \: \: equation}`

`8 = (4)/(5) (2) + b \\ 8 = (8)/(5) + b \\ 40 = 8 + 5b \\ 40 - 8 = 5b \\ 32 = 5b \\ (32)/(5) = b`

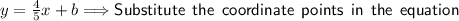
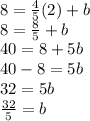
Rewrite the equation by substituting the value of b.

`y = (4)/(5) x + (32)/(5)`

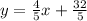
Answer

`\large \boxed{y = (4)/(5) x + (32)/(5) }`