Answer:
Sum of 100 terms of the sequence = 15050
Explanation:
Given expression which represents a sequence is,
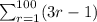
So the sequence will be,
2, 5, 8, 11, 14..........
So, the given sequence is an arithmetic sequence with,
First term of the sequence 'a' = 2
Common difference 'd' = 5 - 2 = 3
Sum of 'n' terms of an arithmetic sequence is given by,
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2022/formulas/mathematics/high-school/d84iitk4llr7wir95u43p7p1ibayc2xect.png)
Here, n = number of terms
a = first term
d = common difference
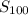 =
=
![(100)/(2)[2(2)+(100-1)(3)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/vn2bm3e0f2ms9697gx8xhnrejgfihqomfs.png)
= 50[4 + 297]
= 15050
Therefore, sum of 100 terms of the sequence = 15050