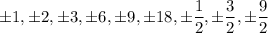Question

Use the Rational Zeros Theorem to write a list of all possible rational zeros of the function.

f(x) = -2x4 + 4x3 + 3x2 + 18

Answer 1

`f(x) = -2x^4 + 4x^3 + 3x^2 + 18\\\\18:\{\pm1;\ \pm2;\ \pm3;\ \pm6;\ \pm9;\ \pm18\}\\2:\{\pm1;\ \pm2\}\\\\Answer:\boxed{\{\pm1;\ \pm2;\ \pm(3)/(2);\ \pm3;\ \pm(9)/(2);\ \pm6;\ \pm9;\ \pm18}`

Answer 2

Answer:
`\pm1 , \pm2 , \pm3 , \pm6 , \pm9 , \pm 18, \pm (1)/(2), \pm (3)/(2), \pm(9)/(2)`

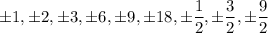
Explanation:

• The Rational Zeroes theorem says that if f(x) has integer coefficients and is a rational zero, then q is the factor of leading coefficient and p is the factor of constant term.

Given polynomial=
`f(x) = -2x^4 + 4x^3 + 3x^2 + 18`

leading coefficient : q = -2

constant term p = 18

Now, Factors of q =
`\pm1, \pm2`

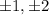
Factors of p=
`\pm1, \pm2, \pm3 ,\pm 6, \pm9, \pm18`

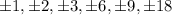
Then , by rational root theorem the rational roots are in the form :

`(p)/(q)=(\pm1)/(1), (\pm1)/(2) , (\pm2)/(1), (\pm2)/(2), (\pm3)/(1), (\pm3)/(2), (\pm6)/(1), (\pm6)/(2), (\pm9)/(1), (\pm9)/(2), (\pm18)/(1), (\pm18)/(2)\\\\\Rightarrow\ (p)/(q)=\pm1 , \pm2 , \pm3 , \pm6 , \pm9 , \pm 18, \pm (1)/(2), \pm (3)/(2), \pm(9)/(2)`

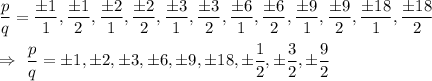
Hence , the list of all possible rational zeros of the function are :

`\pm1 , \pm2 , \pm3 , \pm6 , \pm9 , \pm 18, \pm (1)/(2), \pm (3)/(2), \pm(9)/(2)`