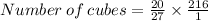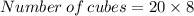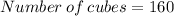Question

A right rectangular prism has these dimensions:

Length − Fraction 1 and 1 over 3 units
Width − Fraction 5 over 6 unit
Height − Fraction 2 over 3 unit

How many cubes of side length 1 over 6 unit are required to completely pack the prism without any gap or overlap?

Answer 1

The number of cubes required is
`160`.

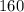Explanation:

The dimensions of the right rectangular prisms are

`l=1(1)/(3) \;units`

`w=(5)/(6) \;units`

`h=(2)/(3) \;units`

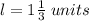
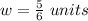
The volume of the right rectangular prism is

`V=l* b* h`.

We substitute the dimensions to get,

`V=1(1)/(3)* (5)/(6)* (2)/(3)`.

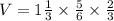We convert the first mixed number to improper fraction,

`V=(4)/(3)* (5)/(6)* (2)/(3)`.

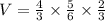We multiply out to obtain,

`V=(40)/(54)`

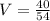
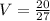`V=(20)/(27)` cubic units.

We need to determine the volume of the cube of side length,

`l=(1)/(6)` units.

The volume of a cube is given by,

`V=l^3`

This implies that,

`V=((1)/(6))^3`

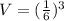
This gives us,

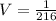`V=(1)/(216)` cubic units.

We now divide the volume of the right rectangular prism by the volume of the cube to determine the number of cubes required.

`Number\:of\:cubes=((20)/(27) )/((1)/(216) )`

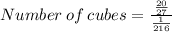
We simplify to get,

`Number\:of\:cubes=(20)/(27) / (1)/(216)`

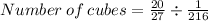
This implies that,

`Number\:of\:cubes=(20)/(27) * (216)/(1)`

`Number\:of\:cubes=20*8`

`Number\:of\:cubes=160`

Answer 2

Volume of rectangular prism = 1 1/3 x 5/6 x 2/3 = 4/3 x 5/6 x 2/3 = 20/27

Volume of cube = 1/6 x 1/6 x 1/6 = 1/216

Number of cubes that will pack the rectangular prism = 20/27 / 1/216 = 160