Question

1 What polynomial identity should be used to prove that 25^2 = (20 + 5)^2 . 2 What polynomial identity should be used to prove that 16^2 = (10 + 6)^2. Possible Answers :. Difference of Cubes. . Difference of Squares. . Square of Binomial. . Sum of Cubes

Answer 1

The answer for the first question is Square of a Binomial because the two terms of the binomial inside the parentheses is equal to 25. The same can be said for the second question because 10 and 6 would also sum up to 16. 

Answer 2

The polynomial identity should be used be Square of Binomial.

To prove

Definition of the Square of binomial

A square binomial is a trinomial that when factored gives you the square of a binomial.

For example, the trinomial x^2 + 2xy + y^2 is a perfect square binomial because it factors to (x + y)^2

`The\ trinomial\ x^(2) +2xy + y^(2)is\ a\ perfect\ square\ binomial\ because\ it\ factors\ to\ (x + y)^2.`

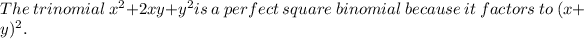
As given

`25^2 = (20 + 5)^2`

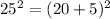
It is written as the trimonial

`25^2 = (20^(2) + 5^2 +2* 20* 5)`

`625= (400 + 25 +200)`

`625= 625`

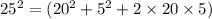
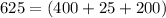
Also

16^2 = (10 + 6)^2

It is written as the trimonial

`16^2 = (10^(2) + 6^2 +2* 10* 6)`

`256 = (100+ 36 +120)`

`256 = 256`

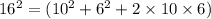
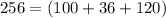
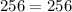
Therefore the Correct answer is Square of Binomial.