Answer
Find out what does the average rate of change of d(t) from t = 2 to t = 5 represent .
To prove
Formula

As given
The distance traveled, in feet, of a ball dropped from a tall building is modeled by the equation d(t) = 16t²
where d equals the distance traveled at time t seconds .
Now
d(5) = 16 × 5 × 5
= 400 feet
d(2) = 16 × 2 × 2
= 64 feet
Now
Change in time = 5 - 2
= 3 second
put all the values in the above formula
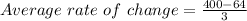

Average rate of change is 112 feet/second.