We cannot agree with Danika. Why? Well, The reasoning is given as follows:
Two functions are inverses of each other if and only if it is true that the composition function is given by:

Everything is ok up to this point, right?. But let's prove that this is not fulfilled for these functions, then:
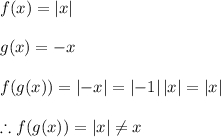
As you can see we did not obtain the function that matches the definition of inverse functions. For that reason we can't agree with Danika.