Answer:
1.

2.
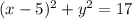
3.
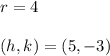
4.
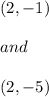
Explanation:
A circle is the set of all points in a plane at a given distance (radius) from a given point (center). The standard equation of a circle with center (h,k) and radius r is given by:

Therefore, we just need to use the previous equation in order to solve the problems.
1. Replacing the data provided into the equation of the circle:
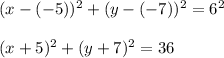
2.
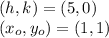
In this case, we have the center of the circle and a point of the circle, so, let's use that information in order to find the radius:
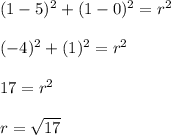
Hence, the equation of a circle with center (5, 0) that passes through the point (1, 1) is:

3. We can extract the solution directly from the equation:

The radius is:
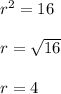
And the center is:

So:
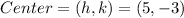
4. We can find one of the points on this circle:
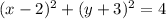
Simply, eliminating one of the variables. For example, let's elimate x evaluating the equation for x=2:
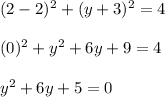
Solving for y:

Hence:
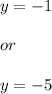
So, two points that are on the circle are:
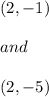
Let's verify it evaluating the points into the equation of this circle.
For (2, -1)
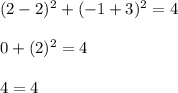
And for (2, -5)
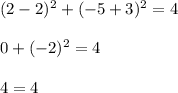
Since they satisfy the equation we can conclude that those points are on the circle.
Additionally I leave you the graph of every circle.