Answer:
The average rate of change of the function over the interval x = 0 to x = 6 is
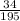 .
.
Explanation:
Geometrically speaking, the average rate of change (
 ) of the function over a given interval is determined by equation of secant line, that is:
) of the function over a given interval is determined by equation of secant line, that is:
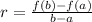 (1)
(1)
Where:
 ,
,
 - Lower and upper bounds.
- Lower and upper bounds.
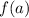 ,
,
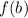 - Function evaluated at lower and upper bounds.
- Function evaluated at lower and upper bounds.
If we know that
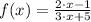 ,
,
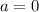 and
and
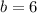 , then the average rate of change of the function over the interval is:
, then the average rate of change of the function over the interval is:
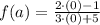
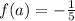
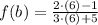
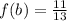
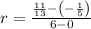
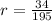
The average rate of change of the function over the interval x = 0 to x = 6 is
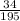 .
.