Final answer:
The height of the antenna is 16 feet.
Step-by-step explanation:
To find the height of the antenna, we can use the Pythagorean theorem.
Let's call the height of the antenna 'h'.
Since the triangle is isosceles, the two sides opposite the equal angles are congruent.
Therefore, the two sides of length 20 ft are equal to each other.
Using the Pythagorean theorem, we can set up the equation:
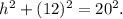
Simplifying, we get:
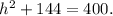
Rearranging the equation, we have:
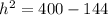
= 256.
Taking the square root of both sides, we find h = 16 ft.
Therefore, the antenna is 16 feet tall.