Answer: The correct option is C) He showed that f(n) ÷ f(n - 1) was a constant ratio.
Step-by-step explanation: Given that Jake has proved that a function f(x) is a geometric sequence.
We are to select the correct method that he used in the proof.
GEOMETRIC SEQUENCE: A geometric sequence is a sequence of numbers where each term is found by multiplying the preceding term by a constant called the common ratio, r.
So, in Jame's proof, he showed that each term is multiplied by a constant to get the next term.
That is, if 'c' is the constant that was used in the proof, then we must have
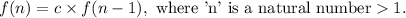
This implies that
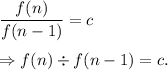
Therefore, he showed that f(n) ÷ f(n - 1) was a constant ratio.
Thus, (C) is the correct option.