Answer:
The statement is false as it depends on the domain
Explanation:
We are given the statement,
For a trigonometric function
 implies
implies
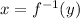 .
.
This statement is not always true.
For example,
The function
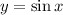 is one-one and onto in the domain
is one-one and onto in the domain
![[-(\pi)/(2),(\pi)/(2)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/gwogv8pom2tu2mge4xip12g2j6aqau5ypk.png) .
.
Thus, its inverse exists in
![[-(\pi)/(2),(\pi)/(2)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/gwogv8pom2tu2mge4xip12g2j6aqau5ypk.png) .
.
That is, in
![[-(\pi)/(2),(\pi)/(2)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/gwogv8pom2tu2mge4xip12g2j6aqau5ypk.png) ,
,
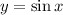 implies
implies
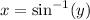 .
.
Hence, we see that,
It depends on the domain for the given statement to be true.
Thus, the statement is false.