Question

What is one of the solutions to the following system of equations?

y2 + x2 = 65
y + x = 7

A (8, −1)
B (1, 6)
C (6, 1)
D (9, −2)

Answer 1

that would be A

check...(8,-1)
y^2 + x^2 = 65
-1^2 + 8^2 = 65
1 + 64 = 65
65 = 65 (correct)

y + x = 7....(8,-1)
-1 + 8 = 7
7 = 7 (correct)

Answer 2

(8,-1)

Explanation:

Given :
`x^(2) +y^(2) =65`

`x+y=7`

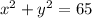
To Find: solution of given system of equations.

Solution:

Equation a :
`x^(2) +y^(2) =65`

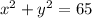
Equation b :
`x+y=7`

Substitute the value of y from equation b in equation a

y from equation b : y = 7-x

Now substitute value of y in equation a

Thus equation a becomes:

`x^(2) +(7-x)^(2) =65`

`x^(2) +49+x^(2)-14x =65`

`2x^(2) -14x =65-49`

`x^(2) -7x -8=0`

`x^(2) -8x+x -8=0`

`x(x-8)+1(x-8)=0`

`(x+1)(x-8)=0`

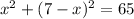
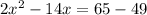
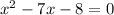
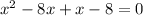
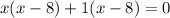
⇒ x= -1 and x = 8

Now substitute values of x in equation b to obtains values of y

⇒
`x+y=7`

for x = -1

⇒
`-1+y=7`

⇒
`y=7+1`

⇒
`y=8`

Thus (x,y)=(-1,8)

For x =8

⇒
`8+y=7`

⇒
`y=7-8`

⇒
`y=-1`

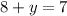
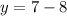
Thus (x,y)=(8,-1)

Hence Option A is the correct solution .