Question

Two quadratic functions are shown.

Function 1:



f(x) = 4x2 + 8x + 1





Function 2:
x g(x)
−2 2
−1 0
0 2
1 8

Which function has the least minimum value and what are its coordinates

Answer 1

The least minimum value is attained by:

First function---- f(x)

Coordinate of the point: (-1,-3)

Explanation:

We are given a equation of first function as:

`f(x)=4x^2+8x+1`

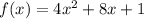
The graph of this function is a parabola which is open upward and the vertex of the parabola is at (-1,-3)

Since, the parabola is open upward hence the vertex of the parabola is the point of minima of the parabola.

The minimum value of the function f(x) is:

-3

Now we are given a table of values of the second function i.e. g(x) as:

x g(x)

−2 2

−1 0

0 2

1 8

Clearly by looking at the values we see that:

The minimum value attained by the function g(x) is:

0

The least minimum value is attained by:

First function--- f(x)

The coordinates of the minimum point are: (-1,-3)

Answer 2

Function 1 written in vertex form is 4(x + 1)^2 - 3 meaning that the vertex is (-1, -3)
Function 2 has a vertex of (-1, 0)
Therefore, function 1 has the least minimum value with cordinates (-1, -3)