Answer:
C
Explanation:
The arc length formula (in radians) is:
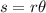
Where,
 is the arc length
is the arc length
 is the radius of the circle
is the radius of the circle
 is the angle intercepted by the arc [in radians]
is the angle intercepted by the arc [in radians]
It is given that radius,
 and angle,
and angle,
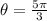
Substituting these values in the arc length formula gives us:
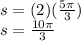
Using
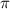 as
as
 and rounding to nearest tenth gives us:
and rounding to nearest tenth gives us:
 ft
ft
Correct answer is C.