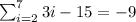Answer:
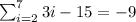
Explanation:
Given :
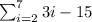
We have to evaluate the given summation.
Consider
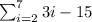
using, we have,

 ..............(1)
..............(1)
Consider,
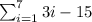
Apply sum rule,
 , we have,
, we have,
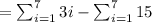
Now, first consider,

Apply constant multiplication rule,
 we have,
we have,
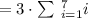
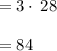
Also,
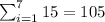
Thus,
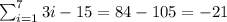
Similarly,
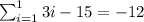
Substitute in (1) , we have,
Thus,
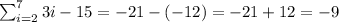
Thus,