Answer:
The area of the enlarged triangle is
 times the original area
times the original area
Explanation:
we know that
The scale factor is equal to divide the measurement of the length side of the enlarged triangle by the the measurement of the length of the corresponding side of the original triangle
In his problem
Let
x------> the length side of the original triangle
so
2x-----> is the length of the corresponding side of the enlarged triangle
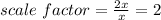
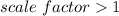 -------> that means is increasing
-------> that means is increasing
The scale factor squared is equal to the ratio of the area of the enlarged triangle divided by the area of the original triangle
so
Let
m-------> the area of the enlarged triangle
n------> the area of the original triangle
r-------> scale factor
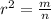
we have

substitute
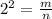

therefore
The area of the enlarged triangle is
 times the original area
times the original area