Question

One night, Gracie was so tired she dreamed about one of her math problems. She dreamed she was on anotherplanet, and some very strange looking monsters lived there. At her school, there were quite a ew blue and purplemonsters, but the yellow-polka-dotted ones with 2 arms and 3 feet seemed to be the most popular. The purplemonsters had 4 arms and 2 feet each, while the blue ones had 5 arms and 4 feet each. Gracie somehow figuredout that there was a total of 173 arms, 175 feet, and 51 heads in the school, not including hers. (Each monsterhas just one head.) Just when she had figured out how many of each kind of monster there were, Gracie’s alarmclock went off, and she couldn’t remember the answer. Can you help her?

Answer 1

Answers:

• 23 blue monsters
• 1 purple monster
• 27 yellow polka-dotted monsters

================================================

Step-by-step explanation:

x = number of blue monsters

y = number of purple monsters

z = number of yellow polka-dotted monsters

x,y,z are positive whole numbers

Let's count the number of heads. We can say

x+y+z = 51

because there are 51 heads from all the monsters combined, and each monster has 1 head.

Now to the number of arms.

• 5x = number of arms from the blue monsters (5 arms each)
• 4y = number of arms from the purple monsters (4 arms each)
• 2z = number of arms from the yellow monsters (2 arms each)

Gracie counted 173 arms in total, so,

5x+4y+2z = 173

Lastly, the number of feet

• 4x = number of feet from the blue monsters (4 feet each)
• 2y = number of feet from the purple monsters (2 feet each)
• 3z = number of feet from the yellow monsters (3 feet each)

She counted 175 feet in total, giving us this third equation

4x+2y+3z = 175

---------------

We have this system of three equations and three unknowns.

`\begin{cases}x+y+z = 51\\5x+4y+2z = 173\\4x+2y+3z = 175\end{cases}`

which honestly seems really tricky to solve.

There are a number of approaches we could take. I'll use substitution.

Let's solve for z in the first equation

`x+y+z = 51\\z = 51-x-y\\`

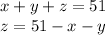
which we can then plug into the other equations.

Plug it into the second equation to get

`5x+4y+2z = 173\\5x+4y+2(51-x-y) = 173\\5x+4y+102-2x-2y = 173\\3x+2y+102 = 173\\3x+2y = 173-102\\3x+2y = 71\\`

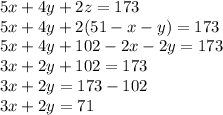
Repeat for the third original equation mentioned

`4x+2y+3z = 175\\4x+2y+3(51-x-y) = 175\\4x+2y+153-3x-3y = 175\\x-y+153 = 175\\x-y = 175-153\\x-y = 22\\`

---------------

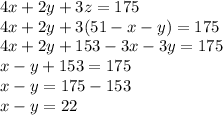
We have this reduced system of equations with two unknowns and two equations this time

`\begin{cases}3x+2y = 71\\x-y = 22\end{cases}`

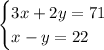
We'll use the same idea as earlier: Solve for one variable, then plug it into the other equation.

Let's solve for x in this new equation 2

`x-y = 22\\x = 22+y`

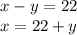
Then plug this into the first equation. Afterward, solve for y.

`3x+2y = 71\\3(22+y)+2y = 71\\66+3y+2y = 71\\66+5y = 71\\5y = 71-66\\5y = 5\\y = 5/5\\y = 1\\`

Then we'll use this y value to find x

`x = 22+y\\x = 22+1\\x = 23\\`

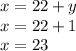
Lastly, we'll use those x and y values to find z

`z = 51-x-y\\z = 51-23-1\\z = 27\\`

---------------

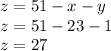
To summarize, we found

• x = 23
• y = 1
• z = 27

This means there are

• 23 blue monsters
• 1 purple monster
• 27 yellow polka-dotted monsters

There's probably a (much) faster way to solve this, but it's not coming to mind at the moment.