Question

The sum of a 3 digit number and a 1 digit number is 217. The product of the numbers is 642. If one number is between 200 and 225, what are the numbers?

Answer 1

Let, the numbers be "x" and "y". Consider "x" as the triple digit number.
Now, according to the question,
x + y = 217..........................equation (1)

x * y = 642............................equation (2)

Now,
Taking equation (2),
x * y = 642
y = 642 / x..................................equation (3)

Now, Taking equation (1),

`x+y=217`

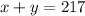
Substituting the value of y from equation (3), we get,


`x+ (642)/(x) =217`


`(x *x+642)/(x) =217`


`x^(2) +642 =217*x`


`x^(2) +642 =217x`


`x^(2) +642-217x =0`


`x^(2) -217x+642 =0`


`x^(2) -3x-214x+642 =0`


`x(x-3)-214(x-3)=0`


`(x-3)(x-214)=0`

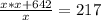
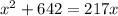
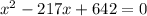
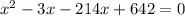
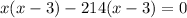
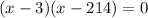
Using zero product property,
EITHER,
x - 3 = 0
x = 3
OR,
x - 214 = 0
x = 214
Since, "x" is the triple digit number, x = 214.
Now,
Taking equation (2),
x * y = 642
Substituting the value of "x" in the equation, we get,
(214) * y = 642
y = 642 / 214
y = 3

So, the numbers are 214 and 3.