Let
x--------> shorter base in yards
y--------> the longer base in yards
z-------> the height in yards
we know that
the area of the flower garden in the shape of a tra-pezoid is


so
 --------> equation
--------> equation

 --------> equation
--------> equation
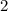
 --------> equation
--------> equation

Substitute equation
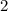 and equation
and equation
 in equation
in equation


![225=(1)/(2) ((z+3)+(z+7))z\\ \\450=[2z+10]z\\ \\2z^(2)+10z-450=0](https://img.qammunity.org/2017/formulas/mathematics/high-school/5dlu48z8uu747te3h8m0vh6tsoueb4xo25.png)
Solve the quadratic equation for z
using a graphing tool
see the attached figure
the solution is
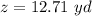
therefore
the answer is
the height of the flower garden in the shape of a tra-pezoid is
