Answer: (28/37) - (48/37)*i
Explanation:
We want to solve the quotient:
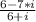
To solve it, we need to multiply the whole quotient by the complex conjugate of the denominator.
Remember that for a complex number:
a + b*i
the complex conjugate is:
a - b*i
Then if the denominatoris:
6 + i
the complex conjugate is:
6 - i
Then to solve the quotient we have:
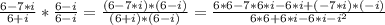
This is equal to:
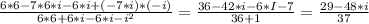
Then the initial quotient is equal to:
(28/37) - (48/37)*i