Question

1.) Solve the following system of equations.

3x - 2y = 6
6x - 4y = 14

(0, 0)
(6, 14)
Infinitely Many Solutions
No Solutions

2.) What is the value of the y variable in the solution to the following system of equations?
5x + 4y = 1
4x + 3y = -1

-7
7
9
-9

3.) Which point lies in the solution set for the following system of inequalities?
y < 2x + 4
y < -2x + 2

(1, 0)
(-5, -2)
(0, -3)
(-1, 5)

Answer 1

Part 1) No solutions

Part 2)
`y=9`

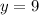
part 3)
`(0,-3)`

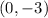
Explanation:

Part 1) we have

`3x-2y=6` -------> equation A

`6x-4y=14` -------> equation B

Multiply the equation A by
`2`

`2(3x-2y)=2*6` -------->
`6x-4y=12`

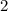
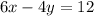
Equation A and equation B represent parallel lines

therefore

Is a inconsistent system of equations

The system has no solution

Part 2) we have

`5x+4y=1` -------> equation A

`4x+3y=-1` -------> equation B

Multiply equation A by
`4`

`4*(5x+4y)=4*1` ------>
`20x+16y=4` ------> equation C

Multiply equation B by
`-5`

`-5*(4x+3y)=-5*-1` ------>
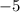
`-20x-15y=5` ------> equation D

Adds equation C and equation D

`20x+16y=4\\-20x-15y=5\\---------\\16y-15y=4+5\\y=9`

Part 3) we have

`y< 2x+4` -------> inequality A

`y< -2x+2` -------> inequality B

we know that

If a ordered pair lie in the solution set of the system of inequalities

then

the ordered pair must be satisfy the system of inequalities

case A)
`(1,0)`

substitute the value of x and the value of y in both inequalities

Verify inequality A

`0< 2(1)+4`

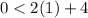
`0< 6` -------> is true

Verify inequality B

`0< -2(1)+2`

`0< 0` ------> is not true

the point
`(1,0)` is not a solution

case B)
`(-5,-2)`

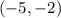
substitute the value of x and the value of y in both inequalities

Verify inequality A

`-2< 2(-5)+4`

`-2< -6` -------> is not true

the point
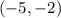`(-5,-2)` is not a solution

case C)
`(0,-3)`

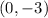
substitute the value of x and the value of y in both inequalities

Verify inequality A

`-3< 2(0)+4`

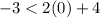
`-3< 4` -------> is true

Verify inequality B

`-3< -2(0)+2`

`-3< 2` ------> is true

the point
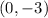`(0,-3)` is a solution

case D)
`(-1,5)`

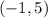
substitute the value of x and the value of y in both inequalities

Verify inequality A

`5< 2(-1)+4`

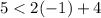
`5< 2` -------> is not true

the point
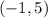`(-1,5)` is not a solution