Answer:
It takes 5.89 seconds for the cannonball to strike the ground
Explanation:
Here,
h(t) = -4.9t² + 27.5t + 8.3
To solve this arithmetically, we just need to set h(t) equal to 0.
So,
-4.9t² + 27.5t + 8.3 = 0
where,
a = -4.9; b = 27.5; c = 8.3
Now, we will use the quadratic formula.
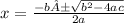
x = -27.5 ± √(27.5)² - 4(-4.9)(8.3) ÷ 2(-4.9)
x = -27.5 ± √756.25 + 162.68 ÷ (-9.8)
x = -27.5 ± √918.9 ÷ (-9.8)
x = -27.5 ± 30.3 ÷ (-9.8)
Now,
x = -27.5 + 30.3 ÷ (-9.8), x = -27.5 - 30.3 ÷ (-9.8)
x = -0.28, x = 5.89
Here, time can't be negative so x = 5.89
t = 5.89
Thus, It takes 5.89 seconds for the cannonball to strike the ground
-TheUnknownScientist 72