Answer:
Part 1:
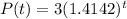
Part 2: There are 24 people infected
Part 3: P(48)=50,331,648
More than 50 million people are infected after 2 days
Explanation:
Exponential Growth
The natural growth of some magnitudes can be modeled by the equation:
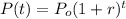
Where P(t) is the actual amount of the magnitude, Po is its initial amount, r is the growth rate and t is the time.
We know the Zika virus started with Po=3 people infected. The number of people infected doubles every 2 hours, which means that for t=2 hours, P(2)=6, thus:
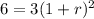
Dividing by 3:
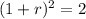
Solving for 1+r:
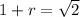
1+r=1.4142
Part 1:
The equation to model the situation is:
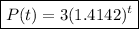
Part 2:
After t=6 hours:
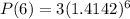
P(6)=24
There are 24 people infected
Part 3:
After 2 days, t=2*24 = 48 hours:
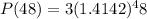
P(48)=50,331,648
More than 50 million people are infected after 2 days