Question

The Zika virus originally started with 3 people. The number of people infected doubles every 2 hours.

Part 1: Write an equation to model the situation.

Part 2: How many people are infected after 6 hours?

Part 3: How many people are infected after 2 days?

Answer 1

Part 1:
`P(t)=3(1.4142)^t`

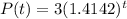
Part 2: There are 24 people infected

Part 3: P(48)=50,331,648

More than 50 million people are infected after 2 days

Explanation:

Exponential Growth

The natural growth of some magnitudes can be modeled by the equation:

`P(t)=P_o(1+r)^t`

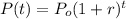
Where P(t) is the actual amount of the magnitude, Po is its initial amount, r is the growth rate and t is the time.

We know the Zika virus started with Po=3 people infected. The number of people infected doubles every 2 hours, which means that for t=2 hours, P(2)=6, thus:

`6=3(1+r)^2`

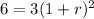
Dividing by 3:

`(1+r)^2=2`

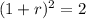
Solving for 1+r:

`1+r=√(2)`

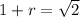
1+r=1.4142

Part 1:

The equation to model the situation is:

`\boxed{P(t)=3(1.4142)^t}`

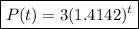
Part 2:

After t=6 hours:

`P(6)=3(1.4142)^6`

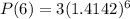
P(6)=24

There are 24 people infected

Part 3:

After 2 days, t=2*24 = 48 hours:

`P(48)=3(1.4142)^48`

P(48)=50,331,648

More than 50 million people are infected after 2 days