Question

Solve the equation. 5t^3 +40t^2 = -80t

a. t= 0 and t= 4
b. t= -4 and t=0
c. t= -4 and t= 5
d. t= 4

Answer 1

Option 'A' is true.

Explanation:

Given the equation

`5t^3\:+40t^2\:=\:-80t`

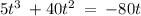
Add 80 to both sides

`5t^3+40t^2+80t=-80t+80t`

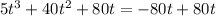
Simplify

`5t^3+40t^2+80t=0`

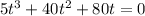
as 5t³ + 40t² + 80t = 5t (t + 4)²

5t (t + 4)² = 0

Using the zero factor principle

if ab=0, then a=0 or b=0 (or both a=0 and b=0)

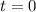`t=0` or
`t+4=0`

solving

`t + 4 = 0`

subtract 4 from both sides

`t+4-4=0-4`

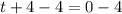
Simplify

`t=-4`

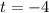
Therefore, the solution to the equation is:

`t=0,\:t=-4`

Hence, option 'A' is true.