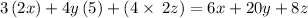Answer:
We conclude that the equivalent expression is:
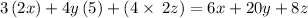
Explanation:
Given the expression
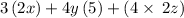
Remove parentheses: (a) = a
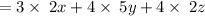
Multiply the numbers: 3 × 2 = 6
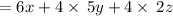
Multiply the numbers: 4 × 5 = 20
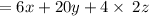
Multiply the numbers: 4 × 2 = 8
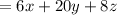
Thus, we conclude that the equivalent expression is: