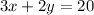
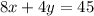

and

In order to solve this systems of equations problem, you need to use the elimination method.
You can multiply the top equation,
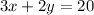 , by -2 in order to eliminate the
, by -2 in order to eliminate the
 values.
values.
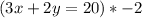 will turn into
will turn into
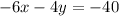
From there, we can eliminate.
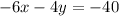
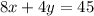
Since
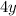 and
and
 are opposites in sign and equal in coefficients, we can remove them from our equations and add the rest of the terms together.
are opposites in sign and equal in coefficients, we can remove them from our equations and add the rest of the terms together.
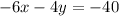
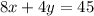
will turn into -->
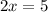
So, x =
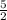 , which means 1 movie costs $2.50. Then, we can solve for the video game price,
, which means 1 movie costs $2.50. Then, we can solve for the video game price,
 , by substituting our x back into one of the equations.
, by substituting our x back into one of the equations.
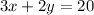
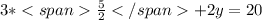
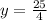
Each movie costs $2.50 and each video game costs $6.25.