Question

Natural gas is stored in a spherical tank at a temperature of 13°C. At a given initial time, the pressure in the tank is 117 kPa gage, and the atmospheric pressure is 100 kPa absolute. Some time later, after considerably more gas is pumped into the tank, the pressure in the tank is 212 kPa gage, and the temperature is still 13°C. What will be the ratio of the mass of natural gas in the tank when p = 212 kPa gage to that when the pressure was 117 kPa gage?

For this situation in which the tank volume is the same before and after filling, which of the following is the correct relation for the ratio of the mass after filling M2 to that before filling M1 in terms of gas temperatures T1 and T2 and pressures p1 and p2?
a. M2/M1= p2T2/p1T1
b. M2/M1= p1T2/p2T1
c. M2/M1= p2T1/p1T2
d. M2/M1= p1T1/p2T2
1. What is the absolute pressure in the tank before filling?
2. What is the absolute pressure in the tank after filling?
3. What is the ratio of the mass after filling M2 to that before filling M1 for this situation?

Answer 1

1. the absolute pressure in the tank before filling = 217 kPa

2. the absolute pressure in the tank after filling = 312 kPa

3. the ratio of the mass after filling M2 to that before filling M1 = 1.44

The correct relation is option c (
`(M_(2) )/(M_(1) ) = (P_(2) T_(1) )/(P_(1) T_(2) )`)

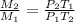Step-by-step explanation:

To find -

1. What is the absolute pressure in the tank before filling?

2. What is the absolute pressure in the tank after filling?

3. What is the ratio of the mass after filling M2 to that before filling M1 for this situation?

As we know that ,

Absolute pressure = Atmospheric pressure + Gage pressure

So,

Before filling the tank :

Given - Atmospheric pressure = 100 kPa , Gage pressure = 117 kPa

⇒Absolute pressure ( p1 ) = 100 + 117 = 217 kPa

Now,

After filling the tank :

Given - Atmospheric pressure = 100 kPa , Gage pressure = 212 kPa

⇒Absolute pressure (p2) = 100 + 212= 312 kPa

Now,

As given, volume is the same before and after filling,

i.e.
`V_(1)` =
`V_(2)`

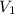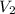
As we know that, P ∝ M

⇒
`(p_(1) )/(p_(2) ) = (m_(1) )/(m_(2) )`

⇒
`(m_(2) )/(m_(1) ) = (p_(2) )/(p_(1) )`

⇒
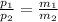
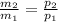
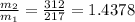`(m_(2) )/(m_(1) ) = (312 )/(217 ) = 1.4378` ≈ 1.44

Now, as we know that PV = nRT

As V is constant

⇒ P ∝ MT

⇒
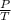`(P)/(T)` ∝ M

⇒
`(M_(2) )/(M_(1) ) = (P_(2) T_(1) )/(P_(1) T_(2) )`

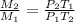
So, The correct relation is c option.