Question

A sample of 18 small bags of the same brand of candies was selected. Assume that the population distribution of bag weights is normal. The weight of each bag was then recorded. The mean weight was 3 ounces with a standard deviation of 0.15 ounces. The population standard deviation is known to be 0.1 ounce.

A.
1. bar x =____.
2. sx =____.
B. In words, define the random variable .
C. In words, define the random variable .
D. Which distribution should you use for this problem? Explain your choice.
E. Construct a 90 confidence interval for the population mean weight of the candies.
i. State the confidence interval.
ii. Sketch the graph.
iii. Calculate the error bound.
F. Construct a 98 confidence interval for the population mean weight of the candies.
i. State the confidence interval.
ii. Sketch the graph.
iii. Calculate the error bound.
G. In complete sentences, explain why the confidence interval in part f is larger than the confidence interval in part e.
H. In complete sentences, give an interpretation of what the interval in part f means.

Answer 1

a)

i. x=- - - - - -

ii. o=- - - - - -

iii. Sx=- - - - -

b) The random variable X signifies the weights of the bags of candies which are selected at random.

c) The statistics variable X is a measure on a sample that is used as an estimate of the population mean.X is the mean weight of the 16 bags of candies that were selected.

d) The distribution needed for this problem is normal distribution with parameters because the population standard deviation is known.

N(X, o/
`√(n)`)

So, the distribution is

N(2, 0.12/
`√(16)`)

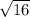e)

i. The 90% confidence interval for the population mean weight of the candies is 1.9589 , 2.0411

iii. The error bound is 0.0411

f)

i. The 98% confidence interval for the population mean weight of the candies is 1.9418 , 2.0582

iii. The error bound is 0.0582

g) The difference in the confidence intervals in part (f) and part (e) is of the level of confidence. The change is, the change in the area being calculated for the normal distribution. Therefore, the larger confidence level results in larger area and larger interval.

Hence the interval in part is larger than the one in part (e).

h) The interval in part (f) signifies that with 98% confidence that the population mean weight of the bag of candies lies between 1.942 ounce and 2.058 ounce.

Explanation:

a)

i. x=- - - - - -

ii. o=- - - - - -

iii. Sx=- - - - -

b) The random variable X signifies the weights of the bags of candies which are selected at random.

c) The statistics variable X is a measure on a sample that is used as an estimate of the population mean.X is the mean weight of the 16 bags of candies that were selected.

d) The distribution needed for this problem is normal distribution with parameters because the population standard deviation is known.

N(X, o/
`√(n)`)

So, the distribution is

N(2, 0.12/
`√(16)`)

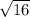e)

i. The 90% confidence interval for the population mean weight of the candies is 1.9589 , 2.0411

iii. The error bound is 0.0411

f)

i. The 98% confidence interval for the population mean weight of the candies is 1.9418 , 2.0582

iii. The error bound is 0.0582

g) The difference in the confidence intervals in part (f) and part (e) is of the level of confidence. The change is, the change in the area being calculated for the normal distribution. Therefore, the larger confidence level results in larger area and larger interval.

Hence the interval in part is larger than the one in part (e).

h) The interval in part (f) signifies that with 98% confidence that the population mean weight of the bag of candies lies between 1.942 ounce and 2.058 ounce.