Question

A quarterback, Patrick, throws a football down the field in a long arching trajectory to wide receiver, Tyreek. The football and Tyreek are traveling in the same direction, started at the same spot, and the football was thrown at the same instant that Tyreek began running. Furthermore, both Tyreek and the football have horizontal components of speed of 22.6 mph. Under these circumstances, no matter what angle the football is thrown at, it will land on Tyreek (whether he catches it or not). True or false

Answer 1

the statement is False
`(x_(ball) )/( x_(rec) )` = cos θ

Step-by-step explanation:

Let's analyze this problem, the ball and the receiver leave the same point and we want to know if at the same moment they reach the same point, for this we must have both the ball and the receiver travel the same distance.

Let's start by finding the time it takes for the ball to reach the ground

y =
`v_(oy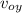)` t - ½ g t²

when it reaches the ground its height is y = 0

0 = vo sin θ - ½ g t²

0 = t (vo sin θ - ½ g t)

The results are

t = 0 exit point

t = 2 v₀ sin θ/g arrival point

at this point the ball traveled

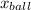`x_(ball)`= v₀ₓ t

x_{ball} = v₀ cos θ 2v₀ sin θ / g

x_{ball}= 2 v₀² cos θ sin θ/ g

Now let's find that distantica traveled the receiver in time

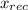`x_(rec)` = v₀ t

x_{rec} = v₀ (2 v₀ sin θ / g)

x_{rec} = 2 v₀² sin θ / g

without dividing this into two distances

`(x_(ball) )/( x_(rec) )` = cos θ

therefore the distances are not equal to the ball as long as behind the receiver

Therefore the statement is False