Question

A nonconducting spherical shell, with an inner radius of 4.0 cm and an outer radius of 6.0 cm, has charge spread nonuniformly through its volume between its inner and outer surfaces. The volume charge density rho is the charge per unit volume, with the unit coulomb per cubic meter. For this shell rho = b/r, where r is the distance in meters from the center of the shell and b=3.0μC/m². What is the net charge in the shell?

Answer 1

the net charge in the shell is 3.7699 × 10⁻⁸ C or 3.7699 × 10⁻² μC

Step-by-step explanation:

Given that;

Inner radius r = 4.0 cm = 0.04 m

Outer radius R = 6.0 cm = 0.06 m

b = 3.0μC/m² = 3.0 × 10⁻⁶ C/m²

we know that volume density = b/r

Now consider spherical shell inside the given shell with radius r and with of dr

the volume of the spherical shell will be;

dv = 4πr².dr

Now total change in this shell will be;

dQ = P.dv

so

dQ = b/r . 4πr².dr

dQ = b × 4πr.dr

Q = 4πb
`\int\limits^R_r {r} \,dx`

Q = 4πb[ r²/2 ]
`^R_r`

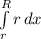
Q = 4πb[ R²/2 - r²/2 ]

Q = 2πb[ R² - r² ]

so we substitute our values

Q = 2π×3.0 × 10⁻⁶[ 0.06² - 0.04² ]

Q = 2π×3.0 × 10⁻⁶ × 0.002

Q = 3.7699 × 10⁻⁸ C or 3.7699 × 10⁻² μC

Therefore, the net charge in the shell is 3.7699 × 10⁻⁸ C or 3.7699 × 10⁻² μC