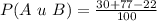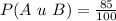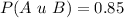Answer
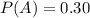
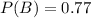
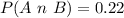
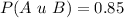
Step-by-step explanation:
Given
See attachment for proper data presentation
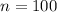 --- Sample
--- Sample
A = Supplier 1
B = Conforms to specification
Solving (a): P(A)
Here, we only consider data in sample 1 row.
Here:
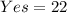 and
and
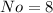
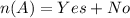
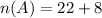
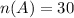
P(A) is then calculated as:
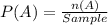
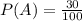
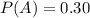
Solving (b): P(B)
We only consider data in the Yes column.
Here:
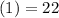
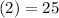 and
and
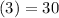
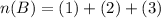

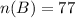
P(B) is then calculated as:
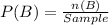
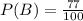
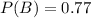
Solving (c): P(A n B)
Here, we only consider the similar cell in the yes column and sample 1 row.
i.e. [Supplier 1][Yes]
This is represented as: n(A n B)

The probability is then calculated as:
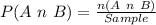
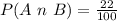
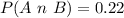
Solving (d): P(A u B)
This is calculated as:
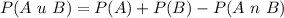
This gives:
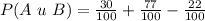
Take LCM