Question

The graph of f(x) = x2 is shifted 3 units down to obtain the graph of g(x). Which of the following equations best describes g(x)?

g(x) = (x + 3)2
g(x) = x2 − 3
g(x) = x2 + 3
g(x) = (x − 3)2

Answer 1

x^2-3[/tex] this is the equation for g(x)

Explanation:

Consider the graph:
`f(x)=x^2`

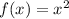
As, we know that moving the function down, you subtract outside the function i.e, f(x)-c ; f(x) moved down c units.

Now, shift the graph f(x) 3 units down to obtain g(x) is,

g(x)=f(x)-3

`g(x)=x^2-3`

Therefore, the equation which best describe for g(x) is ;
`g(x)=x^2-3`

Answer 2

shift up k units, add k to whole function
shift to right h units, add h to every x


f(x)=x^2

3 units down (means -3 units up)
add -3 to whole function
g(x)=(x^2)-3

amswer is the second option