Answer:
Because we know the height of the mailbox is 4 feet and the length is 6 feet, and we also know that it's located 54 feet from the base of the flagpole, we can use proportions to solve the problem.
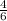 =
=
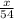
Cross-multiply 4 with 54 and 6 with x to result with 216=6x. Divide 6 to both sides to get 36. So, the height of the flagpole would be 36 feet.