Answer:
Approximately
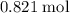 .
.
Step-by-step explanation:
Look up the relative atomic mass of
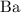 ,
,
 , and
, and
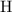 on a modern periodic table:
on a modern periodic table:
Calculate the formula mass of
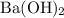 :
:
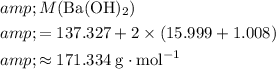 .
.
Calculate the number of moles of
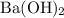 formula units in that
formula units in that
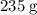 of this compound:
of this compound:
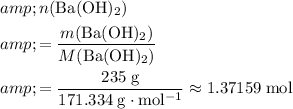 .
.
Calculate the volume of a
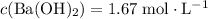 with approximately
with approximately
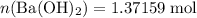 of the solute:
of the solute:
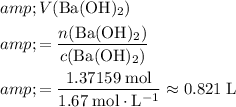 .
.