x = π
STEP - BY - STEP EXPLANATION
What to find?
The solution to the given trigonometric equation.
Given:
3cosx - sin²x + 3 = 0
We first need to note that:
sin²x = 1- cos²x
To find the solution to the given trigonometric equation, we will follow the steps below:
Step 1
Replace sin²x in the given equation by 1 - cos²x.
That is;
3cosx - (1 - cos²x ) + 3 = 0
Step 2
Simplify and re-arrange.
3cosx - 1 + cos²x + 3 = 0
3cosx + cos²x + 2 = 0
cos²x + 3cosx + 2 = 0
Step 3
Let y = cosx
That is;
y² + 3y + 2 = 0
Step 4
Solve the resulting quadratic equation using factorization method.
y² + 2y + y + 2 = 0
y(y+2) + 1( y + 2) = 0
(y + 1)(y + 2) = 0
Either y = -1 or y = - 2
Step 5
Substitute back y=cosx
cosx = -1 or cosx = -2
The only defined solution that we will pick is cosx = -1
Step 6
Find the arc cos of both-side of the equation.
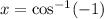
x = 180 degree = π
Therefore, the correct option is π.