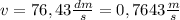Question

A fire hose 5 centimeters in diameter is used to fill a 225-liter bucket. If it takes 15 seconds to fill the bucket, what is the speed at ...

Answer 1

I believe you ask about speed at the end of the hose:

The volume of the bucket is 225 liters which is equal to 225
`dm^(3)`.

`V=225dm^(3)`
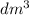
Hose's cross section can be counted with the typical circle's area formula (with diameter instead of radius, that's why you've got a fraction):

`A=3,14*(d^(2))/(4)}=0,19625dm^(2)`


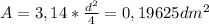
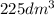
`225dm^(3)` are filled within 15 second.

As the bucket is being filled you can say that it's volume is the volume of the water that flowed out of the hose, then:

`V=A*h`
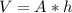
The speed of the water can be counted with equation:

`v=(h)/(t)`
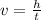
After extracting h from the volume's equation you get:

`v=(V)/(A*t)`
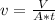
When you count the fraction you get the answer:

`v=76,43(dm)/(s)=0,7643(m)/(s)`