Question

If f(x) = 4 – x2 and g(x) = 6x, which expression is equivalent to (g – f)(3)

Answer 1

`(g-f)(3)=23`

Explanation:

Given :
`f(x) = 4 -x^2` and
`g(x) = 6x`

To find : The value of
`(g -f)(3)`

Solution :

First we find the value of (g-f)

`(g-f)(x)= g(x)-f(x)`

`(g-f)(x)=6x-(4-x^2)`

`(g-f)(x)=6x-4+x^2`

Now, put the value of x=3

`(g-f)(3)=6(3)-4+(3)^2`

`(g-f)(3)=18-4+9`

`(g-f)(3)=23`

Therefore,
`(g-f)(3)=23`

Answer 2

For this case we have the following functions:

`f (x) = 4 - x ^ 2 g (x) = 6x`
The first thing we must do is subtract both functions.
We have then:

`(g - f) (x) = g (x) - f (x)`
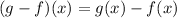
Substituting values we have:

`(g - f) (x) = (6x) - (4 - x ^ 2)`
Rewriting we have:

`(g - f) (x) = x ^ 2 + 6x - 4`
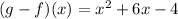
Then, we evaluate the function for x = 3.
We have then:

`(g - f) (3) = 3 ^ 2 + 6 (3) - 4`
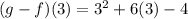
Rewriting:

`(g - f) (3) = 9 + 18 - 4 (g - f) (3) = 23`
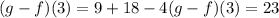Answer:
An expression that is equivalent to (g - f) (3) is:

`(g - f) (3) = 23`