Answer:
B. 1400 meters.
Step-by-step explanation:
According to the statement, there are two stages for the motion of the tractor, in which we need to find the travelled distance:
(i) Uniform accelerated motion.
 (1)
(1)
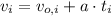 (2)
(2)
Where:
 - Initial position of the tractor, measured in meters.
- Initial position of the tractor, measured in meters.
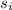 - Final position of the tractor, measured in meters.
- Final position of the tractor, measured in meters.
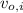 - Initial velocity of the tractor, measured in meters per second.
- Initial velocity of the tractor, measured in meters per second.
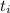 - Time, measured in seconds.
- Time, measured in seconds.
 - Acceleration, measured in meters per square second.
- Acceleration, measured in meters per square second.
 - Final velocity of the tractor, measured in meters per second.
- Final velocity of the tractor, measured in meters per second.
(ii) Uniform motion.
 (3)
(3)
Where:
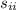 - Final position of the tractor, measured in meters.
- Final position of the tractor, measured in meters.
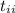 - Time, measured in seconds.
- Time, measured in seconds.
The distance covered by the tractor (
 ), measured in meters, is:
), measured in meters, is:
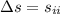 (4)
(4)
If we know that
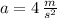 ,
,
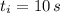 ,
,
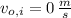 ,
,
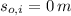 and
and
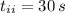 , then distance covered by the tractor is:
, then distance covered by the tractor is:
By (1) and (2):
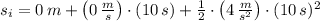
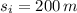
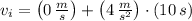
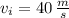
By (3):
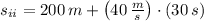
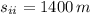
By (4):
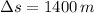
The correct answer is B.