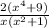1. We need to perform a division by multiplying the dividend with the reciprocal of the divisor. We can apply this rule:
In the problem...
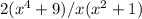
- A =
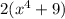
- B = 1
- C =
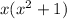
- D = 1
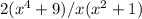 changes to
changes to
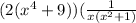
2. We need to get rid of all the parenthesis in this term.
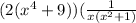
- All negative factors will change the sign.
- In the problem
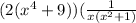 there isn't any negative factors. So the sign will not change.
there isn't any negative factors. So the sign will not change.
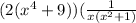 is now
is now

3. Lastly, we need to perform a multiplication.
- We can use this rule:
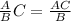
- In the problem
 the new factors on the numerator are:
the new factors on the numerator are:
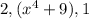
- Notice that all non-fraction factors are placed in the numerator.
- The new factors in the denominator are:
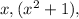
Therefore, the answer is: