- B:
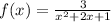
- E:
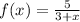
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The domain of a function are the values that the input can assume, in this case, the possible values of x.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer choice A:
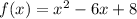
It is a simple quadratic function, with no impediments, so the domain is all real numbers, that is, there are no points that are not in the domain.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer choice B:
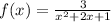
It is a fraction, so the impediment is that the denominator cannot be zero.
The denominator is , and it can be factored as a perfect square trinomial:

It is zero when:
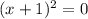
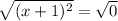
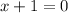

Thus, it has only one point, x = -1, that is not in the domain.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer choice C:

The square root only exists for non-negative values, thus, the domain is:
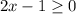


Thus, there are infinite values
 not in the domain.
not in the domain.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer choice D:

Another fraction, and the denominator can be factored as:
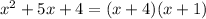
Which is zero at:
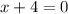 →
→
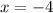
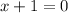 →
→

Thus, it has two points, x = -4 and x = -1, not in the domain.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer choice E:
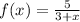
Fraction, the denominator cannot be 0. So
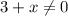 →
→
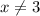
There is one point, x = -3, not in the domain.
Thus, options B and E are selected.